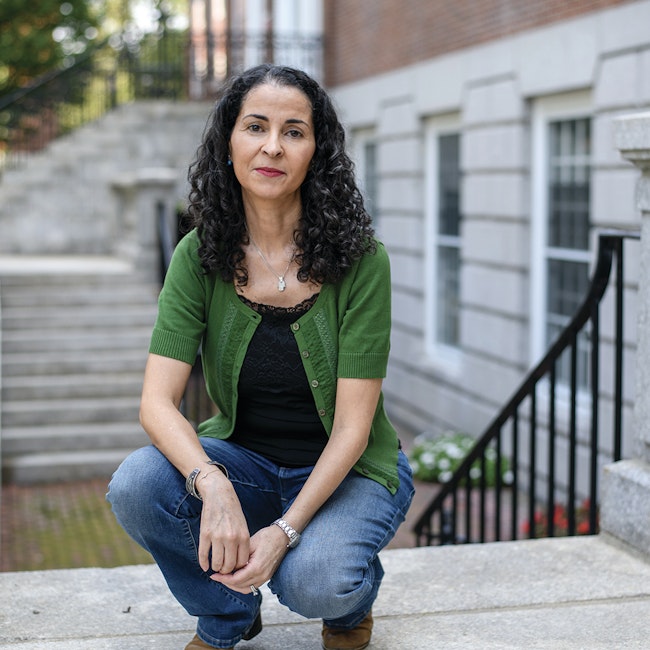Andrea R. Nahmod

This information is accurate as of the fellowship year indicated for each fellow.

Andrea R. Nahmod is a professor of mathematics at the University of Massachusetts at Amherst. Her interests are in two interrelated fields: harmonic analysis, the study of Fourier wave-packet decompositions and frequency interaction analysis; and the theory of partial differential equations (PDE), which models wave-propagation phenomena in nature. In recent years, her research has focused in part on the study of behavior of solutions to nonlinear geometric dispersive equations arising in ferromagnetism and gauge field theories. Dispersive waves are those that spread in space as time evolves while conserving energy.

While at the Radcliffe Institute, Nahmod will focus on the spin-model known as the Ishimori system in the hyperbolic setting and arising in connection to the theories of ferromagnetism and vortex filaments. Because of its relevance to fiber optics, she will also study the standing wave solutions of the associated hyperbolic cubic nonlinear Schrodinger equation. Additionally, she will explore the role of data randomization and the “almost surely” existence of solutions to certain nonlinear dispersive PDE in the periodic setting. She will collaborate with Gigliola Staffilani.

Nahmod holds a PhD in mathematics from Yale University. She was twice a resident at the Institute for Advanced Study in Princeton and at the Mathematical Sciences Research Institute in Berkeley and a professeur invité at the Université Paris-Sud 11. She delivered a plenary address at the American Mathematical Society in 2006 and was the keynote speaker at the Tenth New Mexico Analysis Seminar in 2007. Nahmod’s research is partially funded by the National Science Foundation.