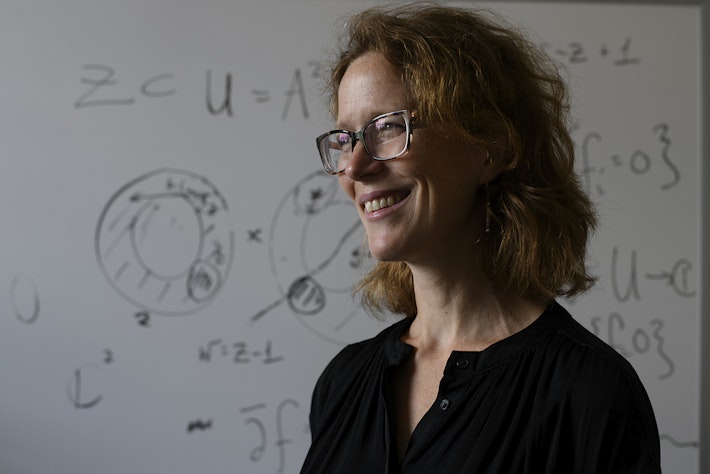Megan M. Kerr

This information is accurate as of the fellowship year indicated for each fellow.

Megan M. Kerr, a differential geometer, is the Clare Boothe Luce Assistant Professor of Mathematics at Wellesley College. Her area of interest is the interplay of group theory and geometry. Kerr studies a class of manifolds in geometry with a high degree of symmetry.

In her Radcliffe fellowship project, titled “Geometry of Symmetric Spaces, Solvable Groups, and Harmonic Manifolds,” Kerr will conduct research in submanifold geometry and Einstein solvmanifolds. Her first investigation involves interpreting solutions to a system of soliton equations corresponding to a symmetric space. Here Kerr’s goal is to study a certain class of submanifolds using techniques from soliton theory. Her second investigation involves finding deformations of Einstein solvmanifolds. Using a method developed in previous work, Kerr proposes to describe the family of Einstein solvmanifold examples “near” a certain hyperbolic symmetric space, which lies within a twelve-dimensional family.

Kerr earned her PhD in mathematics at the University of Pennsylvania, after which she held a John Wesley Young Research Instructorship at Dartmouth College. She has received graduate fellowships from the University of Pennsylvania and the US Department of Education and was a Bunting fellow at Radcliffe.