Episode 204: Math—It’s Not Just Numbers

Photo by Tony Rinaldo

Episode 204: Math—It’s Not Just Numbers, with Laura DeMarco

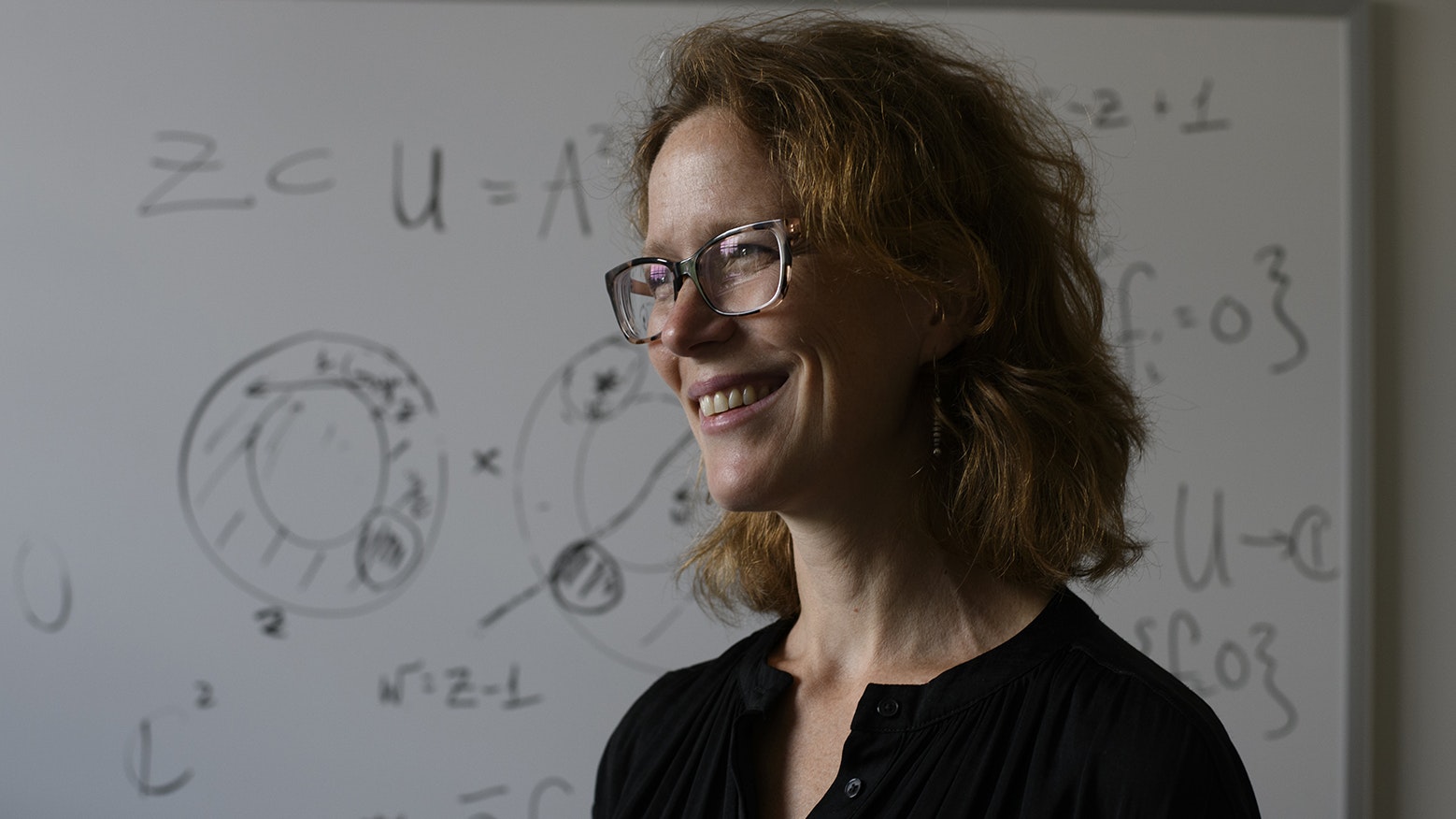
Click on the audio player above to listen to the episode or follow BornCurious on Amazon Music, Apple, Audible, Spotify, and YouTube.

On This Episode

More than addition, subtraction, multiplication, and division, mathematics is a “whole unexplored universe which has no boundaries,” says our guest, Laura DeMarco. In this episode, we reconsider not only what math is but also what it can do—and who can do it.

This episode was recorded on November 9, 2023.
Released on March 14, 2024.

Guest

Laura DeMarco is a Radcliffe Alumnae Professor at Harvard Radcliffe Institute and a professor of mathematics at Harvard University whose research focuses on the theory of dynamical systems and number theory. She is currently investigating the mathematical concepts of stability—if you bump into something, will that knock it out of position?—and complexity, along with how the two are related.

Credits

Ivelisse Estrada is your cohost and the editorial manager at Harvard Radcliffe Institute (HRI), where she edits Radcliffe Magazine.

Kevin Grady is the multimedia producer at HRI.

Alan Catello Grazioso is the executive producer of BornCurious and the senior multimedia manager at HRI.

Jeff Hayash is a freelance sound engineer and recordist.

Marcus Knoke is a multimedia intern at HRI, a Harvard College student, and the general manager of Harvard Radio Broadcasting.

Heather Min is your cohost and the senior manager of digital strategy at HRI.

Anna Soong is the production assistant at HRI.

Transcript

Heather Min:
Welcome back to BornCurious, coming to you from Harvard Radcliffe Institute, one of the world’s leading centers for interdisciplinary exploration. I am your cohost, Heather Min.

Ivelisse Estrada:
And I’m your cohost, Ivelisse Estrada. Today on the show, we are going to tackle advanced mathematics. Before those of you who fear math groan and switch us off, please put aside your algebra trauma long enough to listen, because, to quote Bertrand Russell, the British mathematician, philosopher, and winner of the Nobel Prize in literature, “Mathematics, rightly viewed, possesses not only truth but supreme beauty.”

Heather Min:
Today, we’re excited to talk with Laura DeMarco, one of our Radcliffe Alumnae Professors and a Radcliffe fellow this year. She is also a professor of mathematics here at Harvard and, in that role, a history maker. She’s the third woman—or fourth, depending on how you count—hired to a tenure position in Harvard’s mathematics department. Quick side note, each of the women in the math department have been Radcliffe professors or fellows.

Ivelisse Estrada:
Laura’s research is focused on an area of pure mathematics that bridges two disciplines, the theory of dynamical systems and number theory. So welcome, Laura.

Heather Min:
We are so excited.

Laura DeMarco:
Thank you for having me.

Ivelisse Estrada:
I’m going to ask you this very basic question, which is people make a distinction between arithmetic and mathematics. So what is the difference? Just tell our audience.

Laura DeMarco:
I think that’s a funny question. Mathematicians sometimes use that as a joke, say, “Oh, I’m a mathematician. I’m terrible at arithmetic.” This is a very common thing to hear among mathematicians. But when we say arithmetic, we usually think of the math that we learn as children that we’re learning in elementary school—so addition, subtraction, multiplication, division, and the rules of numbers, of counting numbers, one, two, three, four, so the basic rules of numbers. Maybe the most common example would be something like computing the tip at a restaurant. That’s something that we do every day. So the kind of math that we do every day that you need to do. When we were growing up, people would say, “Oh, you have to know how to balance your checkbook.” Nowadays, people don’t balance a checkbook. They don’t probably use checkbooks anymore.

Ivelisse Estrada:
Except for me. I’m a weirdo.

Laura DeMarco:
No, I do. I still have one too, and I still keep track. But it’s more about computing tip at the restaurant. You know how to quickly do 20 percent or 18 percent or whatever your favorite percentage is. How do you do that? And some people are really quick at that and can do that in their heads, and others cannot. And so that’s arithmetic. But when we think about mathematics, it’s just so much more. It includes that. So I would say yes, that is mathematics too. But for me, mathematics is really so much more. So, for example, we like to think about shape, the difference between round and flat, or concepts of distance. How far away are you from me? Or what is the shortest path from my apartment to the grocery store? Or what is the optimal path from my apartment to the grocery store? Maybe the shortest path means I have to climb a steep hill, and that’s not optimal, and so maybe I want to go around that steep hill.

And thinking about these concepts of distance, and I think that’s geometry, the way things are laid out in space, or going back to numbers. So as I said, basic arithmetic, adding, subtracting, we do a lot of that too. But maybe we’re not just using the numbers that you’re familiar with, the counting numbers. Maybe we’re using other number systems. We’re thinking about the irrational numbers like the square root of two, or transcendental numbers like pi, or complex numbers, where you include the square root of negative one, and we call it i for imaginary, but they’re not imaginary. Well, or maybe all numbers are imaginary. They’re all in our heads. And so we’re thinking about number systems that aren’t just the usual number systems and the rules of them.

Heather Min:
Wait a minute, pi is a transcendental number, and there are—what did you say it was? Irrational number? What? Imaginary? So, okay. When did you learn that there are transcendental numbers and this whole other cosmology of thinking about numbers and how they actually inform the world we live in?

All:
[Laughter]

Heather Min:
Did you go to a special high school?

Laura DeMarco:
I don’t know how to answer this question. [Laughs] No, definitely did not go to a special high school. And I think, in fact, we’re encountering all these other types of numbers all the time, and we just aren’t aware of it. So I mentioned pi because that’s a number that comes up in terms of when we compute the area or the circumference of a circle. And so it’s a number that people are familiar with, and many of them from a very young age.

Heather Min:
May 14th, we celebrate pi day, and we eat a lot of pie.

Laura DeMarco:
March 14th.

Heather Min:
March 14th. Sorry. Yeah.

Laura DeMarco:
3.14159, et cetera. So yeah, I think we’re encountering all these things all the time, but we start to think about them differently as we get more advanced in doing mathematics. And so when we first see algebra, and we’re learning indeed formula, so we learn about something called the quadratic formula, and you’re handed a formula. You want to solve this equation, find its roots, and you’re told to use this formula. And that formula involves a square root, and that’s something new and different. And square root is not something we really usually think about when we’re thinking about counting, but we do start thinking about it when we think about numbers. We have to use numbers that are not just whole numbers or ratios of whole numbers. They’re what we call the rational numbers.

But suddenly, we’re encountering new numbers, irrational numbers. And then we have this whole number line, this thing we call the real number line. We draw it as a line segment with arrows on the end to indicate that it’s going on forever. And there are all those numbers in between all the rational numbers and the whole numbers—and the irrational numbers are just everything that’s not written as a ratio of two whole numbers.

Ivelisse Estrada:
Because you mentioned square roots, and I remember… I’m sure we all read Madeleine L’Engle’s A…

Laura DeMarco:
A Wrinkle in Time.

Ivelisse Estrada:
A Wrinkle in Time. Thank you. And the lead character was always figuring out square roots in her head. And that’s not something that I learned to do in school, and I’ve always been fascinated by that, the fact that she could just sit there and figure out square roots. And I don’t know why that stuck with me. I have not read that book since I was in fifth grade.

Laura DeMarco:
That’s funny. I don’t remember, although I read it to my children relatively recently, in fact, but I don’t— It’s funny. That part didn’t stick with me. Maybe it just seemed a completely normal thing to do. I don’t know.

Ivelisse Estrada:
[Laughs] To a mathematician.

Laura DeMarco:
Yes.

Ivelisse Estrada:
Anyways—

Heather Min:
I’m going to veer to sort of the obvious question that occurs to me, which is, but I’ve got a smartphone, and I’ve got a computer, and all I have to do is find a search engine and type into the browser text field. I don’t even have to do square root of 12. Who gets to do math these days?

Laura DeMarco:
I don’t know if there’s an answer. Anyone gets to do math. It’s a choice that we make that we really—if you want to do more, there’s so much out there, and there’s so much interesting stuff to discover. And I think what people don’t realize is that math is not just what we’re learning in school. Even well beyond arithmetic and including some of the things that I’ve mentioned that mathematics includes, it’s this whole unexplored universe which has no boundaries. We are discovering new mathematics every day, and we need lots of people to help us discover the new mathematics every day, that it’s not this finite box. It’s not this room that you sit in and this is mathematics, and there’s nothing else, and we’re done, and we’ve understood it, and now we just teach it to each other and use it in our computers or anything else.

No, it’s so much more. It’s discovery and exploration, and I think of it a lot an analogy with the way that we’re trying to discover our universe that we’re living in, and we’re sending out probes further and further away from the Earth to see what we can find and exploring with telescopes. And in mathematics, abstractly, we’re doing the same things, just that we’re doing it in conversation with other mathematicians and in our minds. And we’re using computers too, and we’re exploring examples and computations, and new number systems and new shapes, and you can build upon what already exists. And we’re excited to have more people joining us in this party.

Heather Min:
So what are the questions that you are asking that lead you to discover, explore new math?

Laura DeMarco:
Maybe I should start with some examples from the field of math that I’m working in. So mathematics is divided into lots of subfields, is split up into a bunch of areas. Now, the divisions are artificial in the sense that mathematics is really all connected and related, but it helps us organize in our minds what kind of math we’re doing.

Heather Min:
What are some of those?

Laura DeMarco:
Yeah. And so some of the more familiar areas would be things like what we call algebra, which is a subject that has grown out of the algebra that you might’ve seen in school.

Ivelisse Estrada:
Or that I cried over in eighth grade.

Laura DeMarco:
Or that.

Heather Min:
Where we get to mix up Xs and Ys and all those numbers.

Laura DeMarco:
Right. When you use, you’re using the symbols, and you’re studying equations and this sort of simple algebraic equations, polynomials, or geometry. You learn about triangles, you learn about the Euclid axioms, basic geometry in the plane. And so there are aspects of geometry that we’re researching today, and there’s another area which we call analysis, which most people see in its first form as, say calculus, that they learn about the concept of infinitesimals and limits. But I work in an area called dynamical systems at the border with another area which we call number theory. So dynamical systems, it’s the study of things which move, which evolve in time. And examples that I like to use are—our solar system is an example of a dynamical system. You have a sun. You have planets. You have moons. You have gravity. You have relativity. You have all sorts of complicated things as part of your system, and then you try to understand how the objects move in time. And if you take a snapshot of our solar system today, can you predict where the moon will be a hundred years from now, 200 years from now, a million years from now, or billion years from now?

So it’s a question of predictability, and how do we understand this as a system? But another example I want to give, which is much closer to home, and I was thinking of it this morning as I was walking over here because we have all these wild turkeys in our city of Cambridge, and they’re on the street. And I think they’re wonderful, and I even just stopped to take a picture of them. I’ve been living here for three years, and I’ve been seeing the wild turkeys almost every day, and they still make me laugh. And so one might be interested in studying the population dynamics of the wild turkeys in the city of Cambridge. And what does that mean? That means how many are there? Where are they in the city? Where are they living in the summer versus the winter? How is the population? How are the numbers changing?

So what do we do? So we want to say, okay, I’d like to understand how the population of turkeys is evolving over some period of time. And so we try to simplify by saying, okay, maybe I’ll go out and I’ll check once a month. I can’t be watching them all the time. I have to sleep. I have to live my life. I have to eat. But maybe I can go out once a month, and I can count in as many places as possible and see what happens. And so you have these snapshots of what’s happening, just like looking at the planets. You can observe at night. We can’t see them during the day, at least not from here. You might have to go to the other side of the Earth and see them when it’s dark.

And so we have sort of limited observations of our systems. Anyway, so that was all to say that one of the things that I like to do is I’m thinking about a model for what could be a really complicated system, but I want to understand everything about it, and maybe you only have limited information about it. And so you can forget about the real world, come up with some simple formulas that you can study and that you can play with, and you can see how your model evolves in time and try to understand what features of your model are interesting. Which ones are going to persist in the long term? What aspects are unstable if you perturb them in some way? How does the geometry or the shape of the model, the setup that you give it affect the way things behave inside it? So for example, the turkeys: are they confined? We have streets, we have buildings, we have things in our city of Cambridge that restrict where the turkeys can go.

So in my abstract models, I have a particular space that I’m working in. It has a shape. It has a notion of distance itself. It has obstructions. It has barriers. It might have walls in some sense, and then my objects can only move around inside them in a particular way. And I’m trying to understand where do they go and what kind of stable configurations I can find.

Heather Min:
So if I may echo back what I’m hearing: You isolate a particular dynamical system—something, an observed universe or a phenomenon—and you capture what you believe are sort of the essential mechanisms or the observed behavior of it. And so using math, you try to test it and introduce new elements perhaps, as well as things that might disturb that observation of what you recognize it to be an essential property of how it works. And you try to sort of test the limits of it so that you can understand when it is always displaying that behavior, when it turns into something else. And so that’s what I’m hearing. Is that correct?

Ivelisse Estrada:
That’s so funny, Heather, because what I heard was, “I have some formulas about turkeys.”

All:
[Laughter]

Laura DeMarco:
Heather, I think you did a really good job summarizing because I have no formulas about turkeys whatsoever.

Ivelisse Estrada:
Yet.

Laura DeMarco:
Yet.

Heather Min:
So how do you know when something is the right thing to study?

Laura DeMarco:
And that’s such a good question. How do you know what is the right thing to study? This is one of the hardest things to do as a researcher, as a student, and figuring out what aspects are interesting. And it’s hard to answer that because what’s interesting to some people is not interesting to others. But what we want is to understand what’s new. So there’s a lot of, first of all, figuring out what people have already understood. We have some particular collection of examples of systems that we’re interested in studying, and maybe people have seen certain behaviors already. This is not a new field. People have been studying this—this type of mathematics has been around for more than 100 years. It’s not one of the oldest fields. It’s a relatively young field as far as mathematics goes, but it has been studied for about 100 years.

And so we know a lot. So one has to, of course, figure out what’s already been done. But then in any given example, usually everything you’re seeing is new in the sense that you have some example that nobody’s ever looked at. There’s so many examples out there, so many formulas that we could look at, so many particular systems that one could study that it’s often the case that everything about it is new.

Heather Min:
But the universe and the planets and the solar system, that has been around. So why is it new? Why have these questions not been explored?

Laura DeMarco:
From a mathematical point—so there are a lot of observations that have been made about the real world. Oh, there’s a lot of data out there. And what we’re doing as mathematicians is not trying to mimic what we’re seeing the observed reality, necessarily. We want to understand some feature. So for example, I love looking at the images on say, the NASA web page of the rings of Saturn. I think that’s just beautiful. There’s so many things that one could explore about those rings. But one thing you might notice when you look at the pictures is that they’re not completely uniform. It’s not this uniform disc that just are a ribbon that just goes around Saturn. There are gaps in these rings. And what causes those gaps? And there’s the moons, and there’s gravity. But there’s also, if you start Googling this—“What causes the gaps in Saturn’s rings?”—some concept of orbital resonance will pop up when you do a Google search. And you should actually try this.

You just type in, “Why are there gaps in the rings of Saturn?” And the words orbital resonances will pop up. And you’ll say, what on earth is that? Well, I’m not going to answer that question for you right now, but I will say that should be intriguing. And then I’ll say, “Oh, but as a mathematician, that’s what I’m interested in, is the concept of an orbital resonance.” So now, forget about Saturn, forget about the solar system. Let’s say I’m just interested in a function: the function F of X equals X squared plus two or something like this—or X squared minus two, which actually turns out to be more interesting for various reasons.

So I’m interested in studying a function of one variable that has seemingly nothing to do with Saturn and its rings, but I’m interested in taking that function and turning it into a dynamical system, which means what? Which means you start with an initial point, we can call it X, and you plug it into your function, and you get F of X, whatever the value would be. And then you take that output and you stick it back into your function, and you get F of F of X. And you take that output and you stick it back into your function. You get F of F of F of X, and you keep doing this forever and ever. So the process of putting the input and taking the output and returning it back to the input, this is time passing. So this is time now. Time is repeated iteration of this function with some initial starting point and then seeing where it goes in time.

Ivelisse Estrada:
So you just introduced another variable?

Laura DeMarco:
No, there’s still only one. Oh, you mean time?

Ivelisse Estrada:
Yeah.

Laura DeMarco:
If you think of time as a variable, yes.

Ivelisse Estrada:
Okay.

Laura DeMarco:
So in some sense, it’s just one variable. I’m calling it X. It’s some input to my function, but I’m allowing time to pass. But it’s discrete time in the sense that it’s just one, two, three. It’s units, single units of time. And so I’m interested in studying the properties of one of these recursively defined dynamical systems. And when we study these, it turns out that we see gaps in orbits, in some sense similar to what we see in Saturn’s rings.

Heather Min:
Is it correct what I’m hearing, which is that math is the language by which smart people from all over the world use to describe, theorize, and prove what we speculate is how the world works, the universe works? Is there a logic in the universe? And if we try to even posit that, which I’m hearing we are, math is the way to grapple with it, if there is order in the universe.

Laura DeMarco:
That is very difficult for me to answer. So with the type of mathematics I’m doing, although I’m inspired by what’s happening in real life and how people describe the world, I am not myself trying to do that, and so it’s very hard to say if we are really finding the correct language to describe the world that we’re living in, and whether we’re succeeding. And so what we’re doing is we’ve created... We have these fundamental ideas of logic and logical implication and axioms—things that we’re starting with, which are these very universal ideas of logical implication and what it means. And as we build systems or examples or number systems or whatever it is that we’re working with, we want to understand what the logical implications are. And it may turn out that these have nothing to do with the world that we’re actually living in, but it may turn out that they do.

And it’s hard to know whether they will or whether they won’t. And as a pure mathematician and in what I do, I try not to worry about whether it will describe the real world or not, and whether it will have implication. My goal is to understand the systems and the models and the things that we create and their logical implications. I can create a world or a universe that—let’s call my world earth just because that’s a familiar name. We can call it earth, but it’s not really Earth. It’s some system, some abstract system. But it might turn out that the things that I set up inside it will logically imply that earth is flat, that my world is flat. But maybe I create some other... I modify some aspects of my system and it might imply, ah, earth is round, earth is not flat, and which is real.

Well, we have an Earth that we live in, but these are mathematical earths that are not necessarily the same Earth. And so we shouldn’t read too much into all of the logical implications because we’re starting with some simplifying assumptions. And so it’s very difficult to say whether or not my simplified earth is actually modeling the real Earth. The real Earth is very complicated. The real universe is very, very complicated, and we actually can’t really get our hands on everything that’s really out there. There are too many dimensions, too many aspects, too many features, too many parameters, I would say, to consider out there in the real world.

Ivelisse Estrada:
Can I ask a question? Because I know that you are mathematically interested in complexity, but maybe I’m hearing the opposite. There’s so much complexity that it can’t really be studied. So what’s the tension there? And when you study complexity, what does that mean for you?

Laura DeMarco:
Yeah. So one of the things that I’ve gotten very excited about is how complexity or crazy things arise from very, very simple settings. We can start with very simple formulas, a very basic-looking dynamical system and find that there’s already so much richness and so much complexity there that it’s just a surprise. That’s what I mean to say, is that very simple systems give rise to what we call chaotic behavior or high complexity. Complexity can be measured in different ways in mathematics. In a dynamical system, one has the concept of entropy, which is some way that we measure complexity. Entropy can mean a number of different things, in physics or in math, or in different contexts. We have a definition, I’m not going to give you the definition right now. One might be interested in the value of that complexity or entropy in a given system, but the systems can be really simple minded, again, with only one input variable and a very simple formula, and it turns out to exhibit a great deal of complexity.

And so this is beautiful. This is really quite striking, that something that looks very simple... I happened to mention the function earlier, F of X is X squared minus two. This is just a simple looking formula. And maybe in a high school class, you might learn that its graph is a parabola. But if you think of it as a dynamical system and you start iterating, it turns out to be very complicated, and it gives rise to some what we call a chaotic dynamical system, which has positive entropy. In other words, it has complexity, and there’s so much to discover from very, very simple things. So we don’t have to go to the universe. We don’t have to go to the rings of Saturn to find that complexity. We can actually already find it on a very small scale.

But then it’s just mind blowing because then you think, “Oh, if I’m already finding complexity in the function X squared minus two, which looks so simple, how on Earth am I ever going to explore or understand the wild turkeys in Cambridge and their population? Or how am I ever going to understand how the planets are moving around the sun?” Well, maybe we won’t, never will. Maybe we’ll never have a complete mathematical understanding. A mathematical understanding means from start to finish proved, everything is logically implied by something. That’s what we want to do as mathematicians: understand all the mechanisms that explain everything from start to finish. In the real world, in practical life, we don’t need that, is the truth. We don’t need to understand absolutely everything. We can send a rocket spaceship to the moon and back, and we don’t have to have that complete understanding. We have to have enough understanding to be able to do that. And so there are differences.

I worry that I’m digging my own grave here, saying, oh, well mathematicians actually aren’t useful. You don’t really need this kind of mathematics to get along to get by.

Heather Min:
I heard you say that the math that you do cannot be replicated or replaced by artificial intelligence.

Laura DeMarco:
Well, I can’t claim that artificial intelligence will never be able to do what I do because perhaps it will at some point. As it stands today, it cannot.

Heather Min:
What is lacking in AI that is not replicated, or that doesn’t replace what the human mind is doing with math.

Laura DeMarco:
So I’m not an expert in AI, but one thing that I can say is that right now, what a computer can do is only what’s already been done, what’s already been understood, and can only do what it’s trained to do. And right now, we as researchers, we as mathematicians are creating new and inventing new mathematics and discovering new ideas. The computer maybe can point out to me some patterns that I haven’t seen before. So we do spend a lot of time trying to find patterns, and computers can be really helpful with that. If you have a lot of data, for example, or you have examples that you’re trying to compute, the computer can find for you all sorts of interesting patterns and discoveries. But sometimes things might seem like a pattern but is not really a pattern, and you wouldn’t be able to discover that with the computer.

You can run the computer for years, and it will look like a pattern, but maybe it turns out it’s not. And this is what I, as a mathematician want to want to find out. This is what I want to see, is what breaks. When does the pattern break? And that’s fascinating. Certain examples, they seem so simple, and you think that the numbers are going in some kind of sequence. And then wait, there’s something off. And is that an error? Is it a mistake? Or is it for real? And those anomalies are what we grab onto. And earlier, you asked me, what’s interesting? How do we know what’s interesting to study? And it’s when those little dust particles, those things get in the way. There’s something that looks like it’s wrong, but it might not really be wrong. It might be a real feature of the system that you’re looking at that, oh, there’s some pattern.

The pattern has changed—but only after having looked at it for 10 years, or whatever the unit of time is that you’re interested in, that we really want to find the things that the computer can’t see.

Ivelisse Estrada:
I wanted to ask about the role of creativity in mathematics, but it sounds like you need the attention to detail to see where the pattern breaks, and that’s what sets off the creativity. Let me just ask what the role of creativity is in the work that you do.

Laura DeMarco:
I imagine, yeah, it requires a lot of creativity, I suppose, but it’s balanced with a lot of hard work and a lot of practice. And so there’s always this balance of doing a whole lot of learning and practice and getting through material and reading stuff that’s already there. But then, yes, to get past that, to take that next step, one always has to step a little bit away from what’s already been done, and the idea has to come from somewhere.

Ivelisse Estrada:
So how do you do your work? In the movies, we see the mathematician at the blackboard with the chalk, right?

Laura DeMarco:
Yeah. And that’s what we do. Actually, that’s for real. I don’t know. I don’t know which movies you’re thinking of, but in real life, yes. Yes, I spend... So I spend a lot of time thinking and reading what other people have done. But I personally really enjoy talking with other mathematicians and just getting ideas from those conversations, these collaborations. It’s usually just one other person that is having some in-depth conversation that you get into the details of some problem. And yeah, then you jump up to the blackboard, and you explain it to the other person. And then she jumps up to the blackboard, and then she explains it to me. And I have a close collaborator right now. I was just visiting her, and we just spent three very intense days of doing exactly this, of sitting in a room and jumping up to the blackboard and writing down some ideas and writing them on paper. Of course, I mean, that’s the fun part.

That’s the fun part, is thinking about math and thinking, “What’s true?” Thinking, “Wow, we’ve seen all these different examples of some idea, but what are these examples of?” And then, “What’s the limit of what that could be? Which are the examples that don’t fit, and why?” It’s sometimes really subtle. I could be talking about any subject, I realize, right now. There’s nothing specific about mathematics and what I’m saying, but this is what we are doing.

Heather Min:
But it’s the fundamental principle of what you agonize over that you are clarifying for us. And that way, I appreciate why it is called pure math. Let’s pin that right there. Here you are hanging out with all sorts of people as a Radcliffe fellow who are not mathematicians. So how does your exposure and rubbing elbows perhaps inform or color or rub off on the math world that you dwell in, even if it’s just to give you a break from the blackboard?

Laura DeMarco:
It does affect the way I’m thinking about how to communicate what I do to other people. I think it’s really important for people to know what it is to do mathematics. And so here I am sitting with you and realizing, huh, okay, I think agreeing to talk to people about mathematics who are not mathematicians is a really important thing, and it’s really hard. And I’m not sure that I’m succeeding, but I want people to know. I want people to know what it is that mathematicians do, and I want more people to learn about mathematics and to know that it can be done. It’s not for everyone, and I know that. A lot of people say they don’t like it. Maybe they genuinely don’t like it, maybe it’s because they didn’t see enough of it, maybe they could have seen it differently, or maybe they’re just passionate about something else, which is great. But I’d like people to know that it’s out there, that we’re really doing this.

When I was a student in high school, for example, I had never heard of research in mathematics. What is that? Mathematics is just what you’re learning in school, I thought. So I was only in my second year of undergraduate when I learned that, oh, people do research in mathematics. I’ve heard about research in science. People are trying to cure cancer, and scientists are studying the universe, are studying the stars—but what does it mean to do research in mathematics? Oh, maybe it’s also only to help the engineers. Maybe they’re doing the computations for the people that are designing the new race cars. But no, actually, mathematics is... People study it for its own sake and discover mathematics for its own sake. And it’s just amazing that there’s this whole field of discovery and this whole world to explore, and I want people to know that.

Ivelisse Estrada:
I love that. I love that so much. And it also makes me think of this concept of math anxiety, about people getting put off of math from an early age. And I’m wondering whether you have any ideas about what could be done to overcome this concept and get more people excited about math. And let’s say actually even more women or female-identifying people.

Laura DeMarco:
Yes, I wish. Or my own daughter, if only I could get her to be more excited about math. There’s so many things that I wish we could do in our society and in our world that many of them are probably totally impractical. And I wish that students had access to, let’s say, just twice as much mathematics as they do in the schools, because maybe the first half of class could be learning the lessons as they learn. They have to learn how to add. They have to learn how to subtract. They have to do the basic arithmetic, what we started with. But if only they could have yet another hour of math every single day where they’re exploring and playing with shapes and doing discovery and seeing that math is not just about “three plus three is six; three plus four is seven.” That it’s so much more of playing around with ideas and, physically, the shapes that you can play with and things you can build.

And there are just so many tools out there now for children to discover mathematics, but there’s just not time. There’s not time, and I don’t know how to fix that and how to get people beyond their math anxiety. I think a lot of people... People experience mathematics very differently from one another. And indeed, for some people, doing the arithmetic and doing calculations comes very fast and is very easy. And then others think, “Oh, well, I’m not like that, so I’m just not a math person.” But as I was saying, math is so much more than just doing basic arithmetic, and certainly than just doing it quickly. That doesn’t mean that you’re going to be a great mathematician because you can multiply 73 by 135 really fast in your head. I can’t do that. I wish children could discover mathematics the way that we’re actually doing mathematics as this exploratory thing, the way that we learn what research and science is, the way that we see people with test tubes and doing experiments in science or in a lab. We’re also doing...

We have our own laboratories of mathematics. It’s just that we don’t need the same kind of equipment. We can use paper, and we can use models, and we can use cubes and shapes and have math labs.

Ivelisse Estrada:
And you have to be willing to fail over and over again.

Laura DeMarco:
Thank you. Yes, you do. One has to be willing to fail, as it were. Yes, to not know things. And of course, you hear this a lot, we learn from our struggles, and you encounter something you say, “Oh, I really don’t know.” So then let’s look at it more closely if you don’t know. Let’s explore it. Let’s challenge ourselves to try to figure out what that funny feature is. And is it a funny feature, or is it not? And try to explore it more. So yeah, I just wish we had more time to do that. I don’t know what the answer is.

Heather Min:
So we’re really just doing everybody a disservice when math assignments and getting them handed back with a gold star on it, good for you. But that reward is actually quite pale compared to being willing to take the tools and run with it to investigate larger questions.

Laura DeMarco:
Well, I don’t know if it’s a disservice to tell someone, “Hey, great job. You got 100 percent.”

All:
[Laughter]

Laura DeMarco:
I like to get those too. It’s going to make us feel good if we can solve a certain number of problems, but—

Heather Min:
But it’s so much more than that, and most of us stopped too soon, it sounds like. And for you as well, it was only in going to college that the world opened up as far as the possibilities of math. So is it that we just need to stick with it longer for us to get to that point where we have acquired enough tools in that field in order to then really play?

Laura DeMarco:
I think we can play from the beginning. So I don’t think we have to have more years of mathematics before we can get to the playful side of it. I just wish that playful side of it could be incorporated from the start. And it can, and I see that some places are able to do that. Here in Cambridge, we have programs like the Cambridge Math Circle that is run on Saturdays or after school, and there are programs for children that allow them to play with mathematics and discover the beauty of the subject. But it’s outside of school, so it requires extra time and parents that can be committed enough to get their kids to these programs. I really wish that there could be more of the playful aspect of mathematics.

Heather Min:
Do you want to share with us anything about your journey toward being a math professor and a practitioner of the field at a really high level? Why you?

Laura DeMarco:
Yeah, good question. Why me? I think I had a slower start in math and a number of my peers, my colleagues at this level of research mathematics, this group that I’m in, not that they all knew about research themselves necessarily, but a number of mathematicians have gone through, say, camps or programs that exposed them to the concepts of math at an earlier stage, or maybe were doing competitions, math competitions in schools. And I didn’t do those. And in fact, I didn’t think I would be very good at such things. I’d heard of some of the math competitions, but I wasn’t interested, honestly. I was doing other things. I was playing the flute, and I was singing, and I was in theater, and I liked a lot of different things, and I wasn’t committed to doing math. And I also had this perception that—

Heather Min:
I’m not a nerd.

Laura DeMarco:
That’s right. No way. Not me. So yeah, I did other things, but then I was really interested in teaching. I thought I wanted to be a teacher, and I was enjoying my math classes. It seemed to come easily to me. And so I thought, okay, maybe I’ll teach math at some point. And I enjoyed my science classes too. Or maybe I’ll teach science. Who knows? But I went to university, and I mentioned already that then I discovered in my second year that people do research. All of my professors are doing research, all of them. And then that same day that I learned that, I went to all of my professors, and I knocked at their office hour—maybe that week because it couldn’t have all been in one day—but I went to all my professors and I said, “I’ve heard that you do research. Can you tell me about it?”

And they looked at me and thought, “Well, I don’t know if I can really explain what I’m doing to you because don’t know anything, but here: I’ll try.” And it was very awkward and I was embarrassed after, but I was really curious. Really, I had no idea that it wasn’t just the ones in math, it was just all of them were doing research, everybody, even the graduate students, the ones who were the TAs, right? They’re also here to do research. I didn’t know. Thought they were just there to teach.

So that was really eye-opening. The more math I took, the more I realized, oh, I could teach at higher and higher levels, because I was still in my mind thinking that I might want to teach someday. And I am teaching. I am teaching. I’m a professor here at Harvard, and I am teaching students, but the main part of what I do is the research.

And so I think it’s just that the more I got into it, the more I discovered, wow, this is pretty amazing. And I guess we just never know where our path will end up and the things that we discover along the way and what the options are.

Heather Min:
You found your passion, and you’re just doing it.

Laura DeMarco:
And I’m just doing it. And I’m just doing it. And one of the things that I like... So as I said, I wasn’t the competition student, I wasn’t really into solving the problems really fast, and so maybe I can bring different things to the subject, that for me, I’m most excited about finding these connections between different topics,or unexpected connections between different areas or different aspects of mathematics, and making those connections. And I find that really beautiful.

Heather Min:
And you have enough to puzzle through for the rest of your life.

Laura DeMarco:
Oh my goodness, more than my life, my life times 100. Yes, if only I had 100 lives. If only I had a second me that I could double so that I could think about all these different interesting problems and take care of my children and cook dinner. I like to cook, and I just never have enough time to do all of the things that I want to do. I did finally make it to my daughter’s soccer match yesterday. I had missed all of them this season, and I went to the very last one, which was last night.

Ivelisse Estrada:
And it was a major victory.

Laura DeMarco:
And it was in fact a major victory. They won seven to zero. So I was feeling bad for the other team, honestly. So yes, I wish I had more time there. So many interesting problems. It’s truly unlimited. There’s so much to do.

Ivelisse Estrada:
So you came to Harvard from Northwestern University. And there, you took part in a program that was called GROW, Graduate Research Opportunities for Women. And this was specifically in math. Can you tell us more about that?

Laura DeMarco:
Yeah, sure. So as you’re perhaps aware, there aren’t so many women in mathematics. The numbers... Well, we get a decent number of PhDs. I don’t know if it’s now 30 percent of PhDs are awarded to women in mathematics each year—something like that. So that’s not such a low percentage. But one notices that as you get higher and higher into the levels of math and the senior professors at the, what were used to be called the research-one institutions, the top research institutions, there are fewer women. But it’s also been the case that some years, we were getting very few applicants to the PhD programs. So even though some schools were getting a number of women, others were not, or there were fluctuations and the numbers of women that we were getting applying to our PhD program. So GROW, that you mentioned, was a program that was started by my colleague Bryna Kra, who’s also a professor of mathematics, and she’s at Northwestern.

And she had proposed that maybe we need to reach out directly to the students around the US, perhaps even internationally, and let them know at an early stage, that research in mathematics is a thing, that... Like myself, I mentioned earlier, I didn’t know that research in mathematics was even a thing that people do, and I’m probably not alone in that.

Heather Min:
I didn’t know.

Laura DeMarco:
Yeah. So a lot of people just don’t realize that. And what people know is you could do mathematics for other careers. And so there are a number of programs exposing undergraduates to what it means to take mathematics and become some type of scientist or go into industry, or what kind of jobs you can have with a math degree. There are so many jobs you can have. But we wanted to tell the students, oh, there’s also this possibility of doing research in mathematics, and here’s what it’s like.

So we wanted to bring the women or the female-identified students to come and spend a weekend together and explore mathematics and what it would mean to have a career doing research on mathematics, and it was a big success. And so we ran all sorts of surveys after to get a sense of what the students thought, and we tracked them over several years, reached out to them later to find out, did this have an effect on whether or not you’re going to think about doing graduate school in mathematics? And it seemed to indeed have an effect. Certainly, it had a short-term effect at Northwestern. We had very few applications from qualified, strong women students that were interested in a PhD math program. We had very few prior to doing this program, and the numbers went way up. I don’t have them on the tip of my fingertips, so I don’t remember exactly what the numbers were, but it was really striking.

But that was maybe just a local effect, I think. Oh, well, we hosted at Northwestern, and so maybe it was just because we were the hosts that a lot of students applied, but some friends were telling us it seems to be having an effect. And then it went from Northwestern to some other institutions. So it started to spread. And a colleague in England ran one. And most recently, it ran at Duke. There was a GROW program at Duke.

Heather Min:
That sounds terrific, and something that everybody should use and do. That’s exciting.

Ivelisse Estrada:
I don’t think we can close out without asking you a little bit more about your project here, which is about stability. And why don’t you describe it to us.

Laura DeMarco:
So I am studying these very simple looking dynamical systems that are described by say, a function of just one variable. And stability is the question of how, if you change the system a little bit by changing the function, changing the equation just slightly, how that affects the long-term behavior of the system. If some meteor crashes into the Earth, will that affect the orbit of the Earth? Would it affect its nearly perfectly elliptical trajectory? It’s not quite an ellipse, but if you knock it off of that trajectory, would it actually affect it at all? Or if it does affect it, is it going to settle back into its regular path or not? So stability is the question of under perturbation, whether it’s from some external meteor knocking into your planet or something you do where you just change your parameters a little bit from 2 to 2.1, how does that affect the system in the long term?

It might look like it’s going to behave the same for some number of years. But maybe in the forever timeframe, it’s not. It’s going to be completely different in the long term. And I’m interested in how perturbation affects a system. But I look at these relatively simple systems that are defined by algebra, that are defined by polynomial functions. And there, because of the algebra, I can study them not from just traditional dynamical methods, whatever those are. There aren’t really traditional dynamical methods, but there is at least a toolkit. But we can use more tools. Because the equations themselves are algebraic, we can use tools from the subject of algebra. We’ve only really been doing this for, let’s say the last 10 or so years as opposed to the last 100 years of studying systems of this sort. So we have these new tools that we can use. And so I’m specifically interested in how the algebra of these equations affects the orbits and the stability of these equations.

Ivelisse Estrada:
Thank you for that. I just think of somebody walking, and then you push them. Are they going to stumble, or will they keep going forward?

Laura DeMarco:
Right. Yes. How stable is that person as they’re walking down the street? Yes. And so this is the concept of stability. Exactly.

Heather Min:
Well, I feel really excited listening to you, and I am feeling kind of bad just in terms of I think I stopped too soon with math.

Ivelisse Estrada:
Your excitement is infectious, I have to say.

Laura DeMarco:
Oh, it’s so fun. It’s so fun. You should join me at some point. You can join me on one of my projects.

Heather Min:
Thank you very much.

Ivelisse Estrada:
Thank you.

Laura DeMarco:
No, thank you for having me.

Ivelisse Estrada:
BornCurious is brought to you by Harvard Radcliffe Institute. Our producer is Alan Grazioso. Jeff Hayash is the man behind the microphone.

Heather Min:
Anna Soong and Kevin Grady provided editing and production support.

Ivelisse Estrada:
Many thanks to Jane Huber for editorial support. And we are your cohosts. I’m Ivelisse Estrada.

Heather Min:
And I’m Heather Min.

Ivelisse Estrada:
Our website where you can listen to all our episodes is radcliffe.harvard.edu/borncurious.

Heather Min:
If you have feedback, you can email us at info@radcliffe.harvard.edu.

Ivelisse Estrada:
You can follow Harvard Radcliffe Institute on Facebook, Instagram, LinkedIn, and X. And as always, you can find BornCurious wherever you listen to podcasts.

Heather Min:
Thanks for learning with us, and join us next time.